funklion.blogg.se - Draw triangle free pascal

#DRAW TRIANGLE FREE PASCAL CODE#

You'll find this number in the k th column of the n th row of the triangle. In combinations problems, Pascal's triangle indicates the number of different ways of choosing k items out of a total of n. Then you can determine what is the probability that you'd get 1 heads and 2 tails in 3 sequential coin tosses. So if you were going to toss a coin 3 times in a row, there would be 8 possible outcomes of your sequence of heads/tails: H H H, H H T, H T H, T H H, H T T, T H T, T T H, T T T.

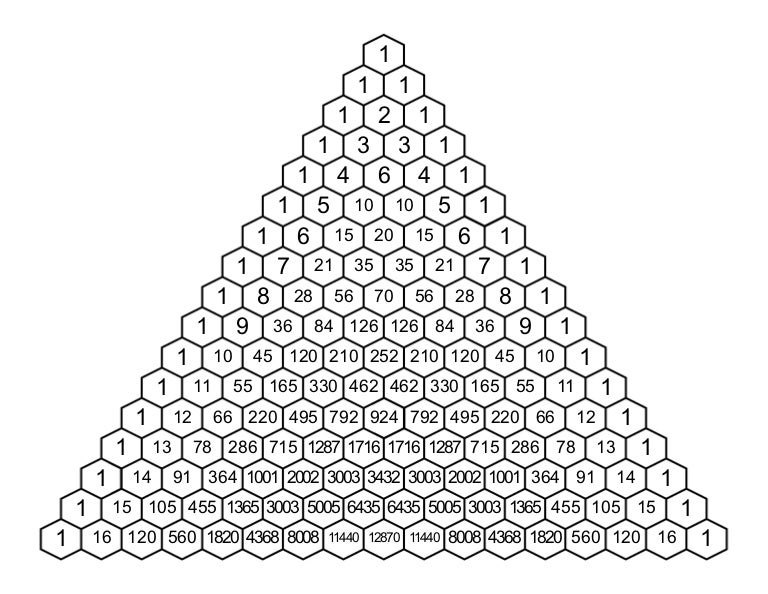
In probability problems, where there is equal chance of either of two outcomes of an event, the total number of outcomes for n events is the sum of the elements in the n th row of the triangle.įor example, sum the numbers in the 3 rd row of Pascal's triangle: 1 + 3 + 3 + 1 = 8. Keep in mind that where there is no coefficient it's the same as having a coefficient of 1. For example if you had (x + y) 4 the coefficients of each of the xy terms are the same as the numbers in row 4 of the triangle: 1, 4, 6, 4, 1. In the binomial expansion of (x + y) n, the coefficients of each term are the same as the elements of the n th row in Pascal's triangle. Pascal's triangle is useful in calculating: Also for any single element the column number is less than or equal to its row number, k ≤ n. So denoting the number in the first row is a 0,0, the second row is a 1,0, a 1,1, the third row is a 2,0, a 2,1, a 2,2, etc. Note that row and column notation begins with 0 rather than 1. Pascal's triangle is triangular-shaped arrangement of numbers in rows (n) and columns (k) such that each number (a) in a given row and column is calculated as n factorial, divided by k factorial times n minus k factorial. If you have any queries regarding this algorithm or flowchart, mention and discuss them in the comments section below.The Pascal's Triangle Calculator generates multiple rows, specific rows or finds individual entries in Pascal's Triangle.

#DRAW TRIANGLE FREE PASCAL CODE#

The algorithm and flowchart for Pascal’s triangle discussed here can be used to write source code for Pascal’s triangle in any high level programming language. Initialize the value of variables, s=n, x=0, y=0, z=s.The sum of the squares of the numbers of row “n” equals the middle number of row “2n”.

The diagonal next to the edge diagonal, in both left and right, contain natural numbers (1, 2, 3, ….) in order.

The sequence of the product of each element or number is related to e, the base of the natural logarithm.

And, all the elements outside the triangle are “0”s.

The edges, left and right, of the triangle consist of “1”s only.

This major property is utilized here in Pascal’s triangle algorithm and flowchart. Again, the sum of 3rd row is 1+2+1 =4, and that of 2nd row is 1+1 =2, and so on. So, the sum of 2nd row is 1+1= 2, and that of 1st is 1.

In Pascal’s triangle, the sum of all the numbers of a row is twice the sum of all the numbers of the previous row.

The triangle starts with a number “1” at the top, and each new number added below the top “1″ is just the sum of the two numbers above, except for the edge which are all “1″s. And, these “0”s are very important for the triangular pattern to work so as to form a triangular array. Most of us who are familiar with Pascal’s triangle don’t know that the numbers outside the triangle are all “0”‘s. Before going through the Pascal’s triangle algorithm and flowchart, here’s a look at it’s properties, and more importantly how the triangle is generated. Pascal’s Triangle is a system of numbers arranged in rows resembling a triangle with each row consisting of the coefficients in the expansion of ( a + b) n for n = 0, 1, 2, 3. The construction of the triangular array in Pascal’s triangle is related to the binomial coefficients by Pascal’s rule. Both the algorithm and flowchart are generate Pascal’s triangle in standard format as per the number of rows entered by the user. In this post, I have presented a simple algorithm and flowchart for Pascal’s triangle along with a brief introduction to Pascal’s triangle, it’s generation mechanism and some of its important properties. Along with the source code, the algorithm and flowchart for Pascal’s triangle is a common problem in any high level language, especially C and C++.